NLP 3주차 심화

심화 RNN / LSTM Model

RNN (Recurrent Neural Network)

등장배경

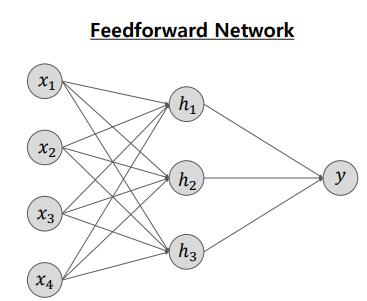
RNN은 피드포워드 신경망 (FeedForward Neural Network,FNN)에서 시계열 데이터의 성질(패턴,순서)을 충분히 학습할 수 없기 때문에 등장하게 되었습니다.

FNN

피드 포워드 신경망은 우리가 알고 있는 가장 기본적인 형태의 신경망입니다. 입력층에서 시작해서 출력층까지 거치면서 각 노드들이 상호작용합니다.

예시로는 MLP , CNN 등이 있습니다.

\[P(w_t | w_{t-1}) = \frac{P(w_{t-1}, w_t)}{P(w_{t-1})} = \frac{P(w_{t-1} \cap w_t)}{P(w_{t-1})}\]

우리는 Bigram 모델에서 다음과 같은 조건부 확률 식을 배웠습니다. 이는 이전 단어 $w_{t-1}$ 로부터 현재 단어 $w_t$ 가 나타날 확률을 의미합니다.
이걸 조금더 확장하면 ,

\[P(w_t | w_{t-1}, w_{t+1}) = \frac{P(w_{t-1}, w_{t+1} | w_t) \cdot P(w_t)}{P(w_{t-1}, w_{t+1})} = \frac{P(w_t \cap w_{t-1} \cap w_{t+1})}{P(w_{t-1} \cap w_{t+1})}\]

이는 중간에 있는 단어를 예측하는 CROW 모델입니다.

즉, 우리는 RNN이 없었던 때는 , 단순히 앞 , 뒤 단어를 통해서 중간에 있는 단어를 예측하거나, 앞의 2개의 단어를 통해서 다음 단어를 예측하는 등 고정된 범위의 단어만을 고려하기 때문에, 먼 문맥을 반영하지 못했습니다. Bigram 모델은 바로 이전 단어 하나만 고려하고 , 트라이그램 모델은 두 개의 앞 단어만 고려하므로, 긴 문맥을 파악하기 어려웠습니다.

n-그램 모델의 한계: n-그램 모델은 고정된 범위의 단어만 고려하기 때문에, 더 먼 문맥을 반영하지 못하고, 데이터가 부족할 경우 sparsity 문제가 발생합니다. 예를 들어, 바이그램 모델은 바로 이전 단어 하나만 고려하고, 트라이그램 모델은 두 개의 앞 단어만 고려하므로, 긴 문맥을 파악하는 데는 한계가 있습니다.

장기 의존성 처리의 어려움: n-그램 모델은 문맥을 고정된 크기만큼만 고려하기 때문에, 문장의 앞부분이나 멀리 떨어진 단어와의 관계를 잘 학습하지 못합니다.

언어 모델이 다루는 사후 확률

언어 모델은 t번째 단어를 타깃으로 하여 t번째보다 왼쪽 단어 모두를 맥락(조건)으로 고려한다
이를 조건부 언어 모델이라고 한다.

\[P(w_1, w_2, \dots, w_{t-1}, w_t, \dots, w_m) = P(w_t | w_1, w_2, \dots, w_{t-1})\]

이 수식에서, $w_{1}$부터 $w_{t}$ 까지 동시에 일어날 확률을 계산하면 곱해야 하기 때문에 동시 확률이다. 동시 확률은 사후 확률의 총곱으로 나타낼 수 있다. (Chain Rule)

\[P(w_1, w_2, \dots, w_m) = \prod_{t=1}^{m} P(w_t | w_1, w_2, \dots, w_{t-1})\]

bigram에 조건부 언어모델 적용

\(P(w_1, w_2, \dots, w_t) = P(w_2 | w_1) \cdot P(w_3 | w_2) \cdot \dots \cdot P(w_t | w_{t-1}) = \prod_{t=1}^{m} P(w_{t+1} | w_t)\) 다음과 같이, 강제로 조건부 언어 모델을 만들 수 있다.
ex) Tom was watching TV in his room. Mary came into the room. Marry said hi to [ ? ]
위 문장에서 ?에 해당하는 부분을 예측할 때, 문맥이 바로 앞의 단어까지만 고려된다고 가정하면, 모델은 to라는 정보만을 바탕으로 예측을 시도합니다. 하지만, 그 이전의 문맥, 즉 Tom이나 TV와 같은 정보는 전혀 고려되지 않습니다.

따라서, 아무리 , 맥락이 길어지더라도, 이를 이해하기 위한 모델의 필요성이 생겨서 길어지는 맥락을 이해할 수 있는 RNN모델이 등장했다.

RNN이란?

RNN(Recurrent Neural Network) 를 직역하면 ‘순환하는 신경망’이다.

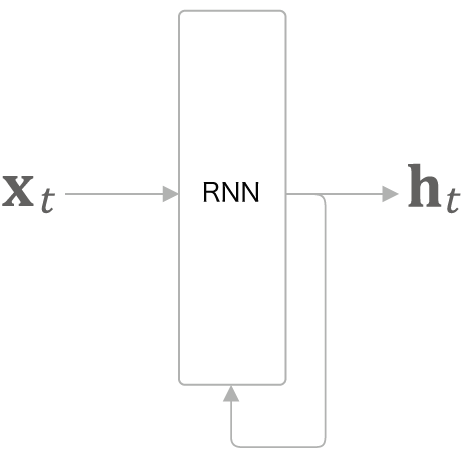
RNN 계층은 위와 같이 표현됩니다. 그림과 같이 RNN 계층은 순환하는 경로를 포함합니다.
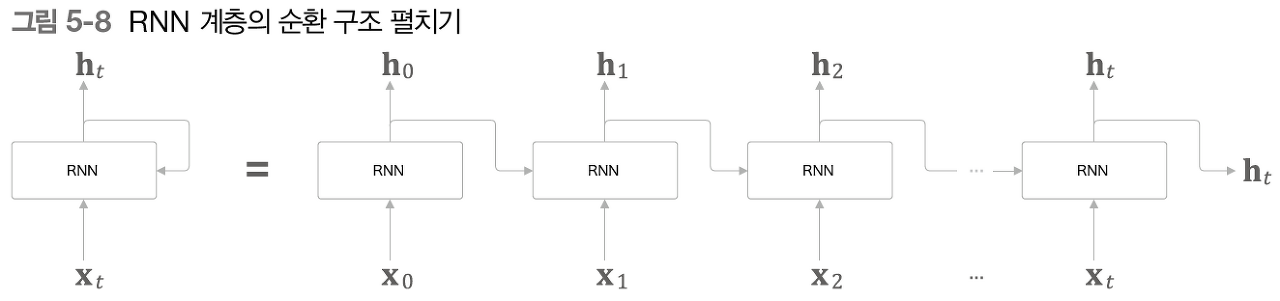
이 순환 경로를 따라 데이터를 계층 안에서 순환시킬 수 있습니다. 그림에서 $x_t$ 를 입력으로 받는데, t는 시각을 의미합니다. 이는 시계열 데이터가 RNN 계층에 입력됨을 표현한 것입니다. 그리고 그 입력에 대응하여 출력 $h_t$(h0, h1, h2 …) 가 나옵니다. 또한, 각 시각에 입력되는 $x_t$ 는 벡터라고 가정합니다. 문장을 다루는 경우를 예로 든다면 각 단어의 분산 표현이 $x_t$ 가 되며, 이 분산 표현이 순서대로 하나씩 RNN 계층에 입력되는 것입니다.

더 자세히 순환 구조 펼쳐보기

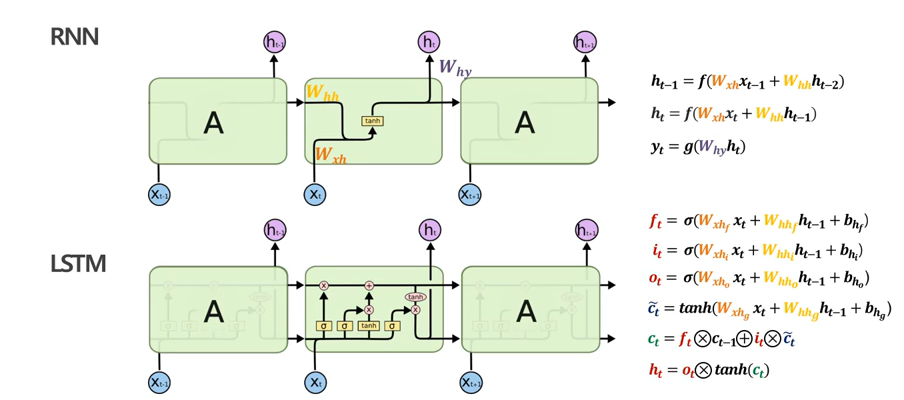
RNN 계층의 수식

1. 은닉 상태 계산

\[h_t = f(W_{xh} x_t + W_{hh} h_{t-1} + b_h)\]

여기서:

• $ h_t $: 현재 시점 $t $에서의 은닉 상태.
• $ h_{t-1} $: 이전 시점 $t-1$에서의 은닉 상태.
• $ x_t $: 현재 시점 $ t $에서의 입력.
• $ W_{xh} $: 입력 $ x_t $와 은닉 상태 $ h_t $ 사이의 가중치 행렬.
• $ W_{hh} $: 이전 은닉 상태 $ h_{t-1} $와 현재 은닉 상태 $ h_t $ 사이의 가중치 행렬.
• $ b_h $: 편향.
• $ f $: 활성화 함수(일반적으로 tanh 또는 ReLU).

2. 출력 계산

\[y_t = g(W_{hy} h_t + b_y)\]

여기서:

• $y_t$: 현재 시점 $ t $에서의 출력.
• $ W_{hy} $: 은닉 상태 $ h_t $와 출력 $ y_t $ 사이의 가중치 행렬.
• $ b_y $: 출력에 대한 편향.
• $ g $: 출력에서 사용하는 활성화 함수(일반적으로 softmax 또는 sigmoid).

BPTT (BackPropagation Through Time)

BPTT는 시간 방향으로 펼친 신경망의 오차역전파법 이라는 뜻입니다.

이 BPTT를 이용하여 RNN모델을 학습한다. 그러나 , 시간 크기가 커지면 역전파 시의 기울기가 불안정해지는 문제가 발생하고, 시간의 크기에 비례하여 컴퓨팅 자원도 증가한다.

이 문제를 해결하기 위해 Truncated BPTT를 사용한다

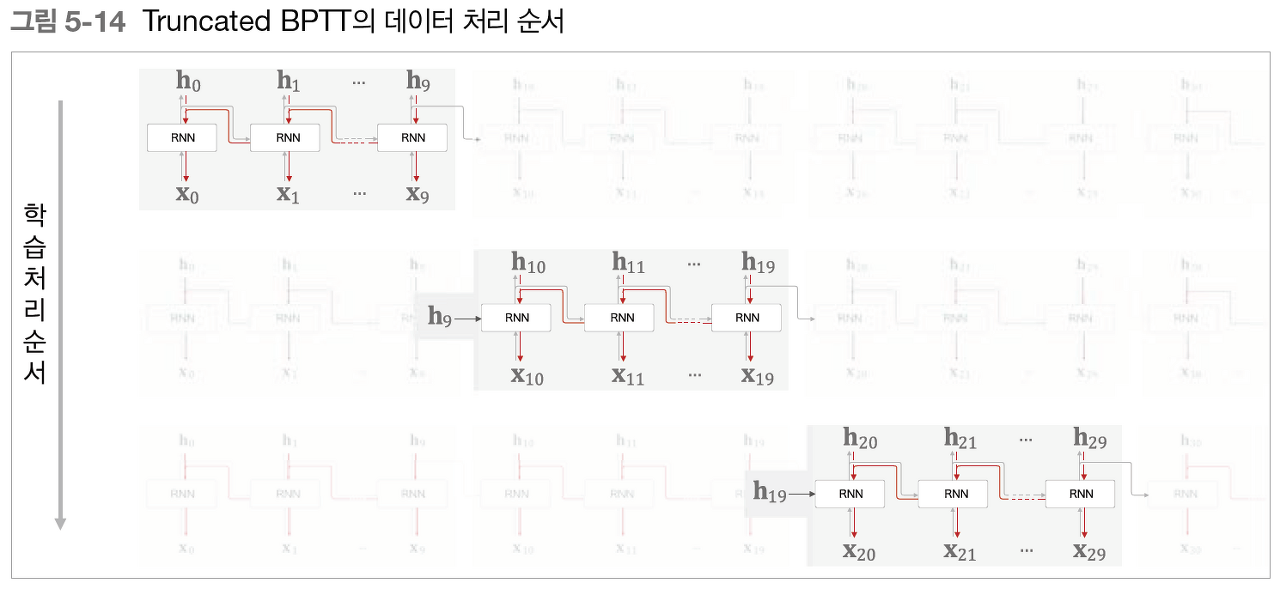
Truncated BPTT

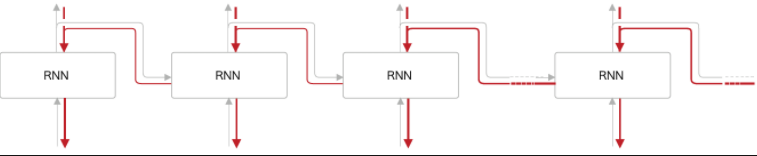
Truncated BPTT는 시간축 방향으로 너무 길어진 신경망을 적당한 지점에서 잘라내어 작은 신경망을 여러개로 만든다. 그리고 잘라낸 작은 신경망에서 오차역전파법을 수행한다.

예시
단어 1000개짜리 말뭉치를 이은다. 즉, 여러 문장들을 이어서 하나의 시계열 데이터로 취급함. 근데 여기서 단어 하나하나가 하나의 계층(Layer)이기 때문에, 1000개의 계층이 만들어진다. 1000개의 계층을 BPTT를 하기에는 계산량과 메모리등이 문제가 된다.

위 그림을 보면 RNN 계층을 길이 10개 단위로 학습할 수 있도록 역전파의 연결을 끊었습니다. 이처럼 역전파의 연결을 잘라버리면, 그보다 미래의 데이터에 대해서는 생각할 필요가 없어집니다. 따라서 각각의 블록 단위로, 미래의 블록과는 독립적으로 오차역전파법을 완결시킬 수 있습니다. 여기서 반드시 기억할 점은 역전파의 연결은 끊어지지만, 순전파의 연결은 끊어지지 않는다는 점입니다. 그러므로 RNN을 학습시킬 때는 순전파가 연결된다는 점을 고려해야 합니다. 즉 데이터를 순서대로 입력해야만 합니다.

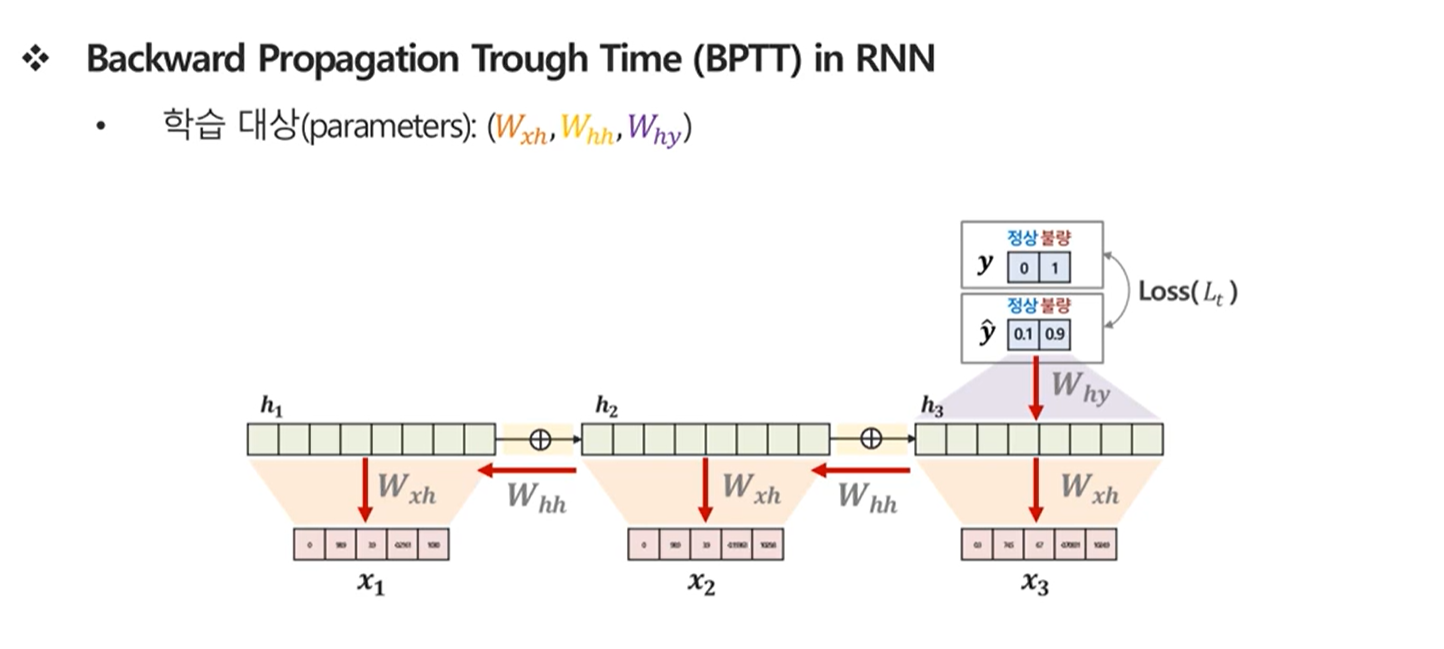
Chain rule을 활용한 Parameter 업데이트

\[\frac{\partial Loss}{\partial W_{hy}} = \frac{\partial L_t}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial W_{hy} h_t} \times \frac{\partial W_{hy} h_t}{\partial W_{hy}}\]

\(\frac{\partial Loss}{\partial W_{hh}} = \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial W_{hh}} + \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial W_{hh}} + \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial h_1} \times \frac{\partial h_1}{\partial W_{hh}}\) dd \(\frac{\partial Loss}{\partial W_{xh}} = \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial W_{xh}} + \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial W_{xh}} + \frac{\partial Loss}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_3} \times \frac{\partial h_3}{\partial h_2} \times \frac{\partial h_2}{\partial h_1} \times \frac{\partial h_1}{\partial W_{xh}}\)

\[W_{hy} \text{의 기여도} = \frac{\partial Loss}{\partial W_{hy}} \\ \Rightarrow W_{hy}^{new} = W_{hy}^{old} - \eta \cdot \frac{\partial Loss}{\partial W_{hy}}\] \[W_{hh} \text{의 기여도} = \frac{\partial Loss}{\partial W_{hh}} \\ \Rightarrow W_{hh}^{new} = W_{hh}^{old} - \eta \cdot \frac{\partial Loss}{\partial W_{hh}}\] \[W_{xh} \text{의 기여도} = \frac{\partial Loss}{\partial W_{xh}} \\ \Rightarrow W_{xh}^{new} = W_{xh}^{old} - \eta \cdot \frac{\partial Loss}{\partial W_{xh}}\]

LSTM

LSTM 등장배경

LSTM은 RNN(Recurrent Neural Network)의 한계점을 극복하기 위해 개발된 모델입니다. RNN의 주요 문제점인 장기 의존성 문제와 기울기 소실 문제를 해결하기 위해 고안되었습니다.

\[W_{hh}^{new} = W_{hh}^{old} - \eta \times \left( \frac{\partial \text{Loss}}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_{t00}} \times \frac{\partial h_{100}}{\partial W_{hh}} + \dots + \frac{\partial \text{Loss}}{\partial \hat{y}_t} \times \frac{\partial \hat{y}_t}{\partial h_{t100}} \times \frac{\partial h_{t00}}{\partial h_{t99}} \times \dots \times \frac{\partial h_{t2}}{\partial h_{t1}} \times \frac{\partial h_{t1}}{\partial W_{hh}} \right)\]

LSTM의 구조

LSTM은 기존 RNN에 없던 몇 가지 핵심 개념을 도입했습니다:

1. 셀 스테이트 (Cell State): 정보를 장기적으로 유지하는 역할을 합니다.(Cell vetor라고 부를 때도 있음. )
2. 세 가지 게이트:
   • 포겟 게이트 (Forget Gate): 어떤 정보를 버릴지 결정합니다.
   • 인풋 게이트 (Input Gate): 어떤 새로운 정보를 저장할지 결정합니다.
   • 아웃풋 게이트 (Output Gate): 어떤 정보를 출력으로 내보낼지 결정합니다.

LSTM의 수식

LSTM의 핵심 수식은 다음과 같습니다:

• 포겟 게이트:
  $f_t = \sigma(W_{xhf} \cdot x_t + W_{hhf} \cdot h_{t-1} + b_f)$

• 인풋 게이트:
  $i_t = \sigma(W_{xhi} \cdot x_t + W_{hhi} \cdot h_{t-1} + b_i)$

• 아웃풋 게이트:
  $o_t = \sigma(W_{xho} \cdot x_t + W_{hho} \cdot h_{t-1} + b_o)$

• 셀 스테이트 후보:
  $\tilde{C}t = \tanh(W{xhg} \cdot x_t + W_{hhg} \cdot h_{t-1} + b_g)$

• 셀 스테이트 업데이트:
  $C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t$

• 히든 스테이트:
  $h_t = o_t \odot \tanh(C_t)$
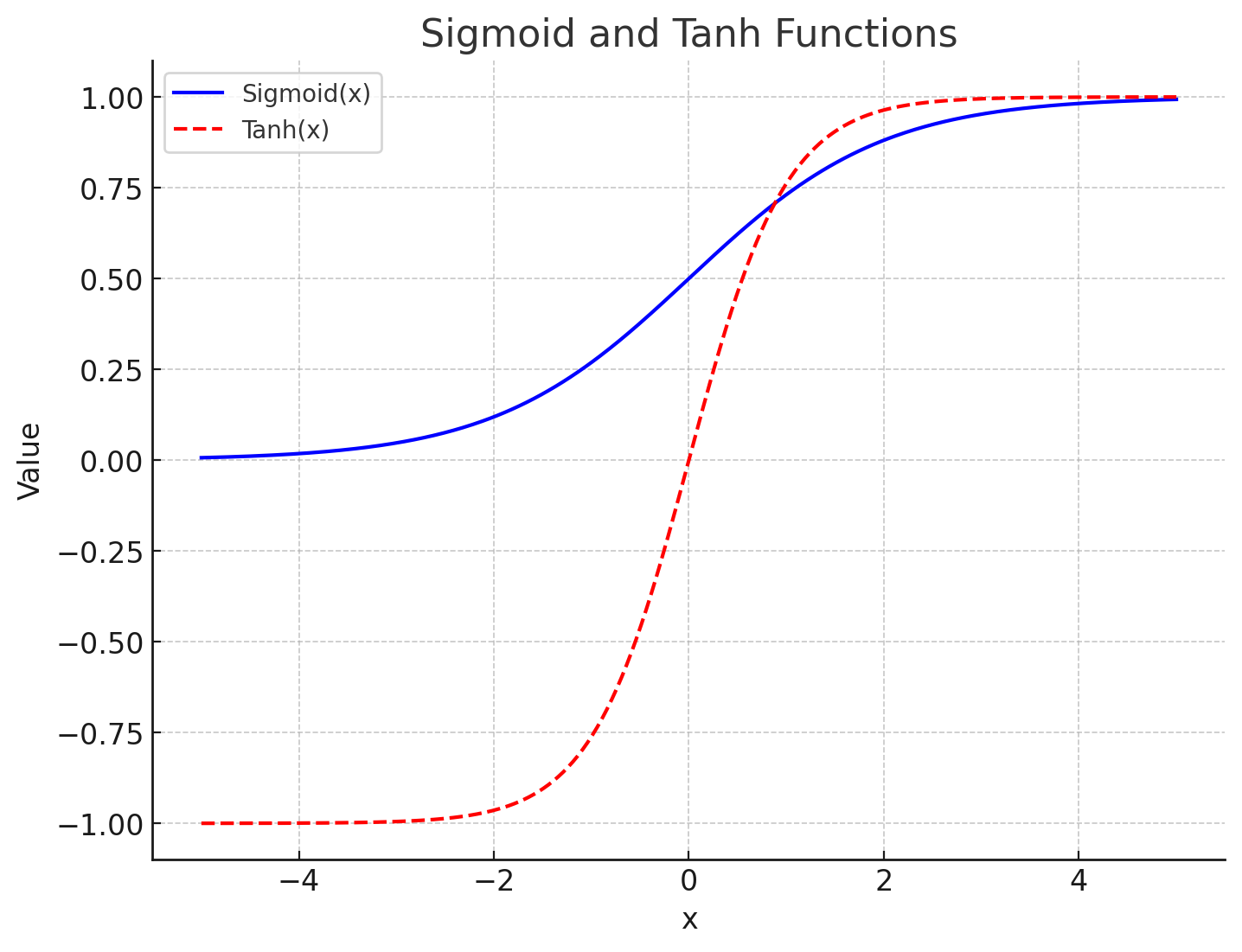
  여기서 σ는 시그모이드 함수, tanh는 하이퍼볼릭 탄젠트 함수를 나타냅니다.

LSTM의 작동 원리

1. 포겟 게이트:
   • 이전 정보 중 어떤 것을 버릴지 결정합니다.
   • 0과 1 사이의 값을 출력하며, 1에 가까울수록 정보를 유지하고 0에 가까울수록 정보를 버립니다.
   • 수식: $f_t = \sigma(W_{xhf} \cdot x_t + W_{hhf} \cdot h_{t-1} + b_f)$
2. 인풋 게이트:
   • 새로운 정보 중 어떤 것을 셀 스테이트에 저장할지 결정합니다.
   • 두 단계로 구성됩니다: a) 시그모이드 층: 어떤 값을 업데이트할지 결정 b) tanh 층: 새로운 후보 값 벡터 생성
   • 수식: $i_t = \sigma(W_{xhi} \cdot x_t + W_{hhi} \cdot h_{t-1} + b_i)$
3. 셀 스테이트 업데이트:
   • 포겟 게이트와 인풋 게이트의 결과를 바탕으로 셀 스테이트를 업데이트합니다.
   • 이 과정에서 장기 기억이 유지됩니다.
   • 수식: $C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t$
4. 아웃풋 게이트:
   • 업데이트된 셀 스테이트 중 어떤 부분을 출력으로 내보낼지 결정합니다.
   • 수식: $o_t = \sigma(W_{xho} \cdot x_t + W_{hho} \cdot h_{t-1} + b_o)$

LSTM vs RNN

LSTM은 RNN과 달리 셀 스테이트를 통해 정보를 장기간 유지할 수 있습니다. 또한, 게이트 메커니즘을 통해 정보의 흐름을 제어함으로써 기울기 소실 문제를 완화합니다.

LSTM의 장점

1. 장기 의존성 문제 해결
2. 기울기 소실 문제 완화
3. 선택적 정보 유지 및 갱신 가능

결론

LSTM은 RNN의 한계를 극복하고 장기 의존성을 효과적으로 처리할 수 있는 강력한 모델입니다. 복잡한 구조에도 불구하고 다양한 시퀀스 데이터 처리 작업에서 우수한 성능을 보여주고 있습니다.

용어 풀이

시퀀스 데이터란?
시퀀스 데이터는 연관된 연속(순서가 있는)의 데이터를 지칭하며 소리, 문자열, 주가 등의 데이터를 나타낸다.

은닉층(hidden layer) -> 책이나 논문에서 $h(x)$ 로 많이 활용
목적: 은닉층은 입력 데이터를 변환하고, 중간 계산을 수행하는 역할을 합니다. 입력층에서 받은 데이터를 여러 차례의 변환을 거쳐, 출력층에서 원하는 결과를 만들 수 있도록 돕습니다.
출력: 은닉층의 출력은 다음 은닉층이나 출력층에 전달되는 값입니다. 즉, 외부로 직접적으로 나타나지 않고, 신경망 내부에서만 사용됩니다.
활성화 함수: 보통 비선형 활성화 함수(예: ReLU, tanh)를 사용하여 복잡한 패턴을 학습할 수 있도록 합니다. 은닉층의 활성화 함수는 신경망이 선형적이지 않은 변환을 학습할 수 있게 해줍니다.
기능: 데이터의 특징을 추출하고, 패턴을 찾아내며, 입력 데이터를 고차원 공간으로 변환합니다. 신경망이 복잡한 문제를 풀 수 있게 해주는 핵심 역할을 합니다.

출력층(output layer)
목적: 출력층은 은닉층에서 전달된 최종 정보를 기반으로 예측 결과를 제공합니다. 이는 신경망이 풀고자 하는 문제의 답(예: 분류 결과, 회귀값 등)을 결정하는 역할을 합니다.
출력: 출력층의 값은 최종 결과로, 신경망이 학습한 결과를 외부에 전달합니다. 예를 들어, 분류 문제라면 각 클래스에 속할 확률이나 예측된 클래스를 출력하게 됩니다.
활성화 함수: 출력층의 활성화 함수는 문제의 유형에 따라 다릅니다.
분류 문제: softmax (다중 클래스 분류)나 sigmoid (이진 분류)가 주로 사용됩니다.
회귀 문제: 활성화 함수 없이 선형 출력(예: identity function)을 사용하는 경우가 많습니다. 기능: 출력층은 예측된 값을 전달하고, 이 값은 손실 함수(예: 크로스엔트로피, 평균제곱오차)와 비교되어 모델의 성능을 평가하고 학습하는 데 사용됩니다.

활성화 함수(activition function ) 정리

층	활성화 함수	용도 및 설명	수식
출력층	시그모이드	이진 분류에서 0과 1 사이 확률을 출력	\(f(x) = \frac{1}{1 + e^{-x}}\)
	소프트맥스	다중 클래스 분류에서 각 클래스에 속할 확률을 출력, 합이 1이 됨	\(f(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}}\)
	항등 함수	회귀 문제에서 연속적인 값을 출력, 값이 그대로 출력됨	\(f(x) = x\)
은닉층	ReLU	0보다 큰 값을 그대로 출력, 0보다 작은 값을 0으로 출력	\(f(x) = \max(0, x)\)
	tanh	입력을 -1에서 1 사이로 변환, 중간 값이 0이므로 학습에서 더 균형적	\(f(x) = \tanh(x)\)
	시그모이드	0과 1 사이로 변환, 깊은 신경망에서는 잘 사용되지 않음	\(f(x) = \frac{1}{1 + e^{-x}}\)

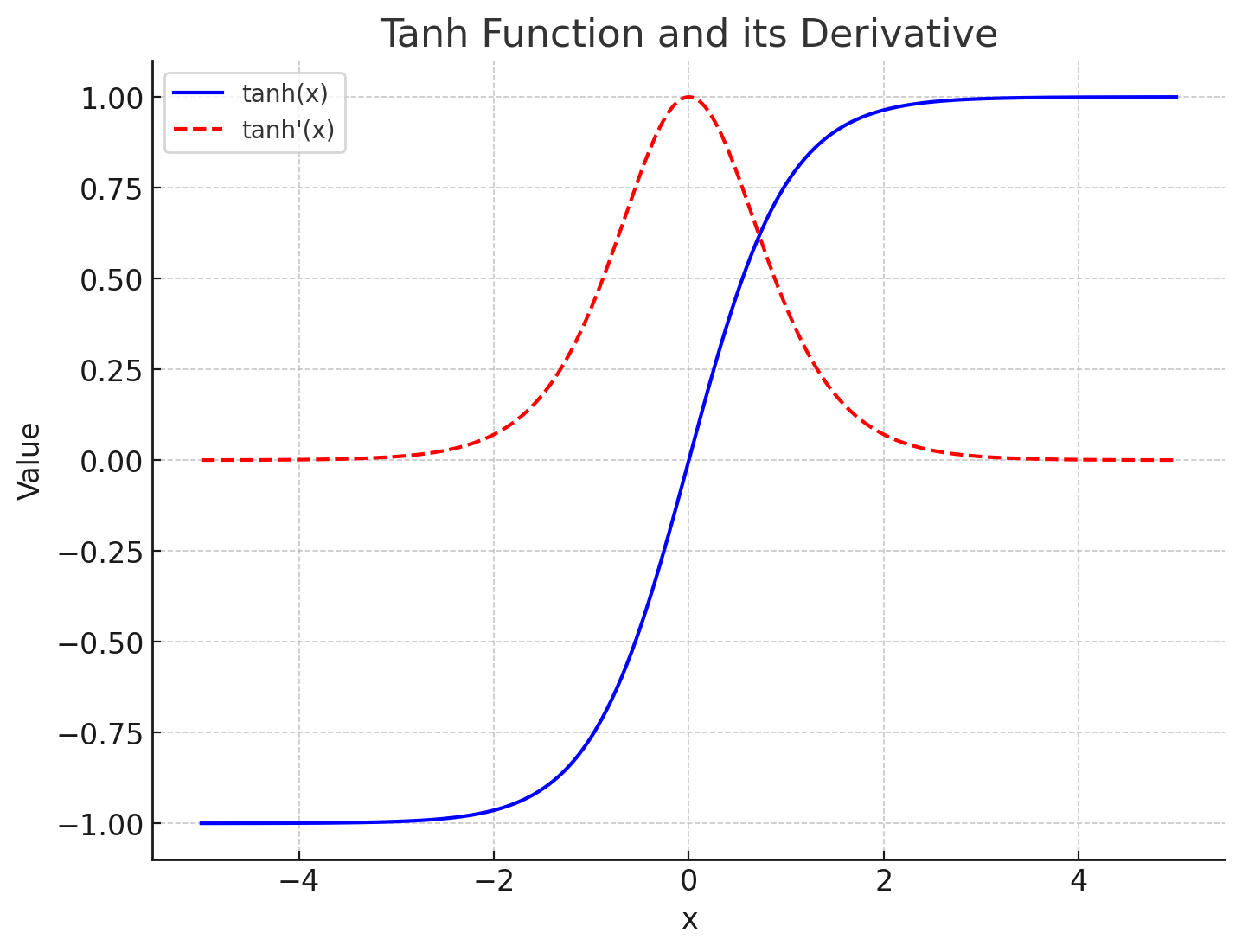
Sigmoid VS tanh