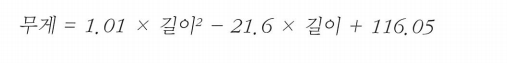Regression Analysis

Posted Aug 1, 2024 Updated Aug 10, 2024

By SangYubLee

17 min read

Regression Analysis

Chapter3. 회귀 알고리즘과 모델 규제

k-최근접 이웃 회귀

지도학습(Supervised Learning)은 분류(Classification)와 회귀(Regression)로 나뉜다. k-최근접 이웃 분류 알고리즘은 가까운 샘플 k개를 선택하여 새로운 샘플의 클래스를 예측함.
k-최근접 이웃 회귀는 회귀이기 떄문에 이웃한 샘플의 타깃이 어떤 클래스가 아니라 수치를 예측함.

1.데이터셋 불러오기

perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0, 21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7, 23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5, 27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0, 39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5, 44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0, 1000.0])

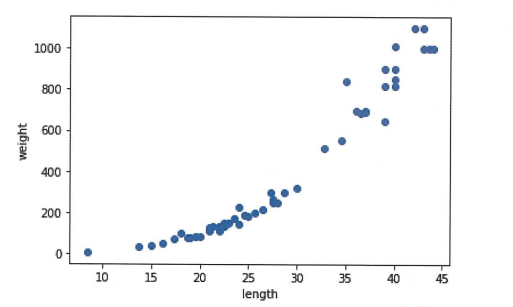
2.산점도 그리기

import matplotlib.pyplot. as plt
plt.scatter(perch_length,perch_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

3.trainset과 validationset 나누기

from sklearn.model_selection import train_test_split
train_input, test_input,train_target,test_target = train_test_split(perch_length,perch_weight,random_state=42)
test_array = test_array.reshape(2,2) #(2,2)행렬로 변환 
print(test_array.shape)

사이킷런에 사용할 훈련 세트는 2차원 배열이어야 한다.

Numpy는 배열의 크기를 자동으로 지정하는 기능을 제공함. 크기에 -1을 지정하면 나머지 원소 개수로 모두 채우라는 의미이다.

train_input = train_input.reshape(-1,1)
test_input = test_input.reshape(-1,1)
print(train_input.shape,test_input.shape)

결정계수($R^2$)

회귀에서 정답을 맞힌 개수의 비율을 결정계수(cofficient of determination)이라고 부른다 이를 $R^2$이라한다. $R^2 =1-(타깃-예측)^2/(타깃-평균)^2$

from skleanr.neighbors import KNeighborsRregressor
knr=KNeighborsRegressor()
knr.fit(train_input,train_target)
print(knr.score(test_input,test_target)) #knr에서 scoresms 결정계수임 

> 0.9928094061010639

MAE(절댓값 오차 평균)구하기

from skleanr.metircs import mean_absolute_error
test_prediction = knr.predict(test_input)
mae=mean_absolute_error(test_target,test_prediction)
print(mae)

> 19.157142857142862

과대적합 vs 과소적합

과대적합은 훈련 세트에서 점수가 굉장히 좋았는데 테스트 세트에서 점수가 나쁜 모델
과소적합은 훈련세트보다 테스트 세트의 점수가 높거나 두 점수 모두 낮은 모델

print(knr.score(train_input,train_target)

> 0.9698823289099255

현재 과소적합이기 때문에, 이를 해결해야함. 해결 방법은 k의 개수를 줄여서 모델을 복잡하게 만들 수 있다. 이웃의 개수를 줄이면 훈련 세트에 있는 국지적인 패턴이 민감해지고, 이웃의 개수를 늘리면 데이터 전반에 있는 일반적인 패턴을 따를 것이다.

knr.n_neighbors = 3
knr.fit(train_input,train_target)
print(knr.score(train_input,train_target))

>0.974645996398761 #결과가 과소적합 해결함. 

선형회귀

k-최근접 이웃의 한계를 풀어보자.

데이터 불러오기 및 전처리

import numpy as np
from sklean.model_selection import train_test_split 
from skleanr.neighbors improt KNeighborsRegressor
#데이터 불러오기 
perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0, 21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7, 23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5, 27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0, 39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5, 44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0, 1000.0])

#2차원 배열로 바꾸기
train_input,test_input,train_target,test_target = train_test_split(perch_length,perch_weight,random_state=42)
train_input = train_input.reshape(-1,1)
test_input = test_input.reshape(-1,1)

#모델 학습
knr = KNeighborsRegressor(n_neighbors=3)
knr.fit(train_input,train_target)
print(knr.predict([[50]]))

> 1033.3333333

50cm의 농어무게는 1,033g보다 훨씬 많이 나감. 이 문제를 선형회귀로 지금부터 풀 것임. 일단 산점도부터 그려보자

import matplotlib.pyplot as plt 
distances,indexes = knr.kneighbors([[50]]) #50cm 농어의 이웃을 구한다
plt.scatter(train_input,train_target) #훈련 세트의 산점도를 그린다
plt.scatter(train_input[indexes],train_target[indexes],marker='D')#훈련 세트 중에서 이웃 샘플만 다시 그림
plt.scatter(50,1033,marker='^')
plt.show()

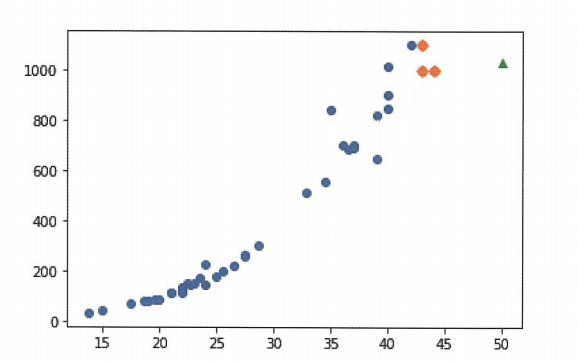k-nn에서 문제는 50cm 농에서 가장 가까운 것은 45cm근방이기 때문에 k-nn알고리즘은 이 샘플들의 평균을 구했다.

print(np.mean(train_target[indexes]))

>1033.33333333

산점도를 그려서 확인해보기

distasnces,indexes = knr.kneighbors([[100]])
plt.scatter(train_input,train_target)
plt.scatter(train_input[indexes],train_target[indexes],marker='D')
plt.scatter(100,1033,marker='^')
plt.show()

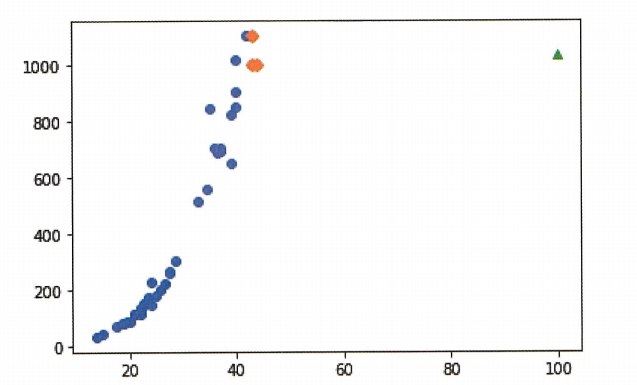knn 알고리즘의 한계 직면! 다른 알고리즘으로 풀어야할 것
머신러닝 모델은 한 번 만들고 끝나는 프로그램이 아니다. 시간과 환경이 변화하면서 데이터도 바뀌기 때문에 주기적으로 새로운 훈련 데이터로 모델을 다시 훈련시켜야 한다. 예를들어 배달음식이 도착하는 시간을 예측하는 모델은 배달원이 바뀌거나 도로 환경이 변할 수 있기 때문에 새로운 데이터를 사용해 반복적으로 훈련해야 한다.

선형회귀

from skleanr.linear_model import LinearRegression
lr=LinearRegression()
lr.fit(train_input,train_target) #선형회귀 모델 훈련 
print(lr.predict[[50]])#50cm 농어에 대한 예측

> [1241.83860323]

coef,intercept보는 코드

print(lr.coef_,lr.intercept_)

> [39.01714496] -709.0186449535477

coef_와intercept_를 머신러닝 알고리즘이 찾은 값이라는 의미로 모델 파라미터(model parameter)라고 부른다.

산점도 그려보기

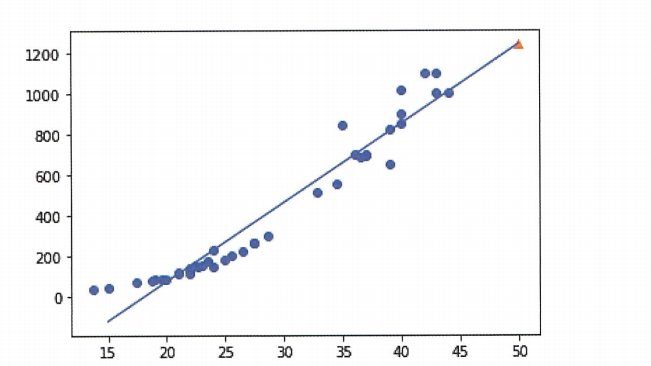
plt.scatter(train_input,train_target)
plt.plot([15,50],[15*lr.coef_+lr.intercept_,50*lr.coef_+lr.intercept_])
plt.scatter(50,1241.8,marker='^')
plt.show()

$R^2$ 확인

print(lr.score(train_input,train_target)) #훈련 세트 
print(lr.score(test_input,test_target)) #테스트 세트

>0.9398463339976039
>0.8247503123313558

다항회귀

농어의 길이와 무게에 대한 산점도를 자세히 보면 일직선이라기 보다는 왼쪽으로 조금 구부러진 곡선에 가깝다. 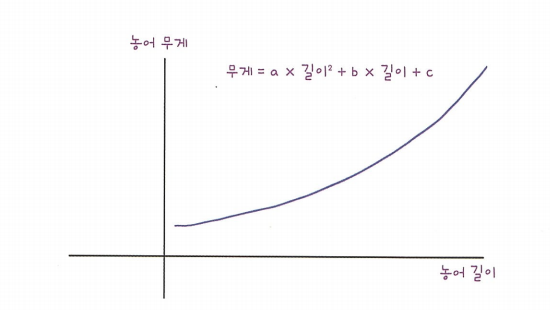농어의 길이를 제곱해서 원래 데이터 앞에 붙여야된다.
1 2 3 train_poly=np.column_stack((train_input**2,train_input)) test_poly =np.column_stack((test_input**2,test_input)) print(train_poly.shape,test_poly.shape)
1 > (42,2) (14,2)
-이 데이터를 통해 다시 모델 훈련
1 2 3 lr =LinearRregression() lr.fit(train_poly,train_target) print(lr.predict([[50**2,50]])
1 > [1573.98423528]
1 print(lr.coef_,lr.intercept_)
1 [1.01433211 -21.55792498] 116.0502107827827
이 결과가 뜻하는 것은 이런 방정식을 다항식이라 부르며 다항식을 사용한 선형 회귀를 다항회귀라고 부른다.

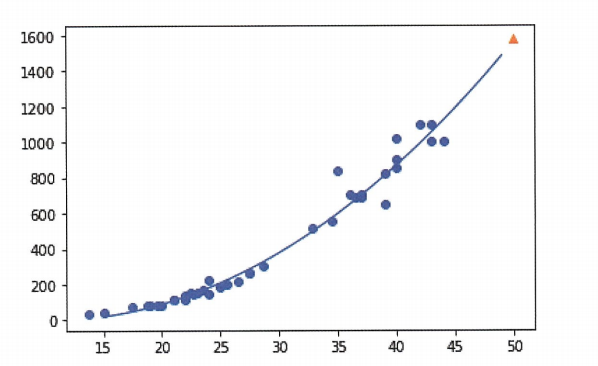
산점도 그려보기

point=np.arange(15,50)
plt.scatter(train_input,train_target)
plt.plot(point,1.01*point**2 -21.6*point+116.05)
plt.scatter([50],[1574],marker='^')
plt.show()

모델 평가
1 2 print(lr.score(train_poly,train_target)) print(lr.score(test_poly,test_target))
1 2 >0.9706807451768623 0.9775935108325122
결과를 보면 훈련셋,테스트 셋에 대한 점수가 높아짐 그러나, 여전히 과소적합이 남아있다. 더 복잡한 모델이 필요.

특성 공학과 규제

특성공학이란 기존의 특성을 사용해 새로운 특성을 뽑아내는 작업이다.
예를 들면, $농어길이*농어높이$와 같이 새로운 특성을 만듦. 사이킷런을 사용하면 쉽게 할 수 있음.

다중회귀

다중회귀란 여러 개의 특성을 사용한 선형 회귀 모델이다. 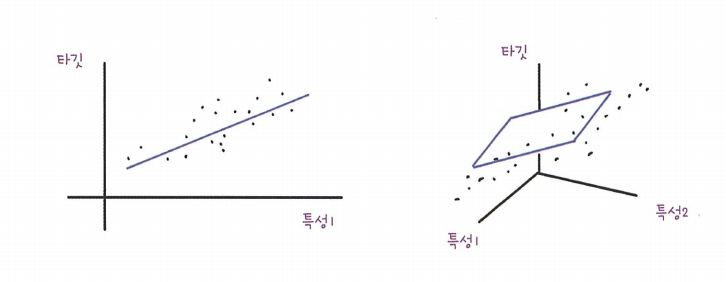단순회귀모델은 직선이고 2개면 평면을 학습한다.

오른쪽과 같이 특성이 2개면 타깃값과 함께 3차원 공간을 형성하고 선형 회귀 방정식 $타깃=a특성1+b특성2+절편$이 된다.

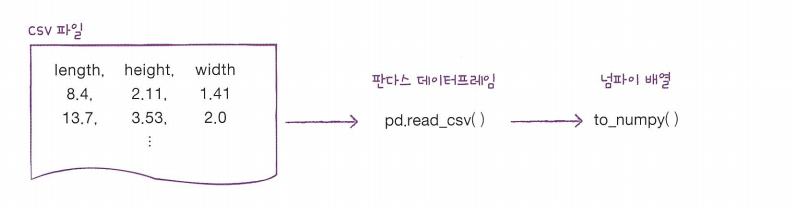
1.Pandas를 활용한 데이터 준비

-다음과 같은 과정을 통해 데이터를 처리한다.

import pandas as pd
import numpy as np
df = pd.read_csv('https://bit.ly/perch_csv')
perch_full=df.to_numpy()
print(perch_full)
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0, 1000.0])

2.훈련 데이터셋과 테스트 셋으로 나누기

from sklearn.model_selection import train_test_split
train_input,test_input,train_target,test_target = train_test_split(perch_full,perch_weight,random_state=42)

사이킷런의 변환기

사이킷런은 특성을 만들거나 전처리하기 위한 다양한 클래스를 제공한다. 사이킷런에서는 이런 클래스를 변환기라고 부른다. 사이킷런의 모델 클래스에 일관된 fit() , score() , predict() 메서드가 있는 것처럼 변환기 클래스는 모두 fit(),trainsform()메서드를 제공한다.

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures()
poly.fit([[2,3]])
print(poly.transform([[2,3]]))

> [[1. 2. 3. 4. 6. 9.]]

transform전에 꼭 poly.fit을 사용해야 하나요?
훈련(fit)을 해야 변환(transform)이 가능하다. 두 메서드를 하나로 붙은 fit_transform 메서드도 있음!

변환기는 입력 데이터를 변환하는 데 타깃 데이터가 필요하지 않다. 따라서 모델 클래스와는 다르게 fit()메서드에 입력 데이터만 전달했다. 즉 여기에서는 2개의 특성(원소)을 가진 샘플[2,3]이 6개의 특성을 가진 샘플 [1. 2. 3. 4. 6. 9.]로 바뀌었다. 즉 6개의 특성으로 $2*3$되었다.
사이킷런의 선형 모델은 자동으로 절편을 추가함. 즉, include_bias=False를 지정하지 않아도 됨.

poly = PolynomialFeatures(include_bias=False) #절편을 위한 항이 제거되고 특성의 제곱과 특성끼리 곱한 항만 추가 됨.
poly.fit([[2,3]])
print(poly.transform([[2,3]])) 

> [[2. 3. 4. 6. 9.]]

이 방식을 train_input에 적용

poly=PolynomialFeatures(include_bias=False)
poly.fit(train_input)
train_poly=poly.transform(train_input)
print(train_poly.shape)

> (42,9) #이 결과는 9개의 특성이 만들어짐

poly.get_features_names() #9개의 특성이 각각 어떤 입력의 조합으로 만들어졌는지 알 수 있음

> ['x0','x1','x2','x0^2','x0x1','x0x2','x1^2','x1x2','x2^2]

test_poly = poly.transform(test_input)
#테스트 셋 변환

다중 회귀 모델 훈련하기

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_poly,train_target)
print(lr.score(train_poly,train_target))

> 0.9903183436982124

print(lr.score(test_poly,test_target))

> 0.9714559911594134

3제곱,4제곱등은 PolynomialFeatures클래스의 degree 매개변수를 추가해서 가능

poly= PolynomialFeatures(degree=5,include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = polt.transform(test_input)
print(train_poly.shape)

이를 활용하여 선형 회귀 모델을 다시 훈련시킴.

lr.fit(train_poly,train_target)
print(lr.score(train_poly,train_target))

> 0.999999999

print(lr.score(test_poly,test_target))

> -144.40579242684848

특성의 개수를 늘리면 선형 모델은 강력해짐. 그러나, 과적합이 일어남으로 테스트 셋에서 형편없는 점수가 나옴.

규제

규제는 머신러닝 모델이 훈련 세트를 과도하게 학습하지 못하도록 훼방하는 것을 말한다. 선형회귀 모델의 경우 특성에 곱해주는 계수의 크기를 작게 만드는 일이다.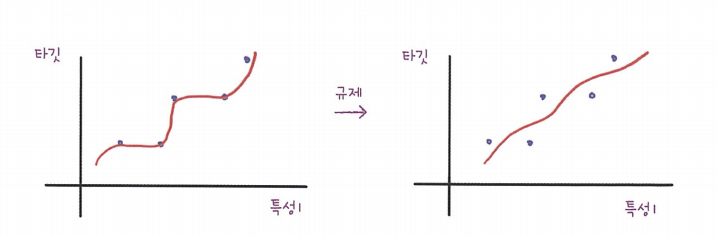

규제를 통해서 훈련 세트의 점수를 낮추고 테스트 세트의 점수를 높일 수 있음 선형 회귀 모델에 규제를 추가한 모델을 릿지(ridge)와 라쏘(lasso)라고 부른다. -릿지(ridge)는 계수를 제곱한 값을 기준으로 규제 를 적용 함 -라쏘(lasso)는 계수의 절댓값ㅇ르 기준으로 규제를 적용함.
일반적으로 릿지를 더욱 선호함 이유는 라쏘는 계수의 크기를 아예 0으로 만들 수 있기 때문이다.
특성간에 스케일이 다르기 때문에 정규화를 먼저 해야함

from sklearn.preprocessing import StandardScaler
ss=StandardScaler()
ss.fit(train_poly)
train_scaled = ss.transform(train_poly)
train_scaled = ss.transform(test_poly)

이제 표준 점수로 변환한 train_scaled와 test_scaled가 준비 됨.

릿지 회귀

from sklearn.linear_model import Ridge
ridge=Ridge()
ridge.fit(train_scaled,train_target)
print(ridge.score(train_scaled,train_target))

> 0.9896101671037343

print(ridge.score(test_scaled,test_target))

0.9790693977615398 테스트 세트 점수가 정상으로 돌아옴. 확실히 많은 특성을 사용했음에도 과적합이 일어나지 않음.
릿지,라쏘 모델을 사용할때 매개변수 alpha를 사용할 수 있음. alpha가 커지면 규제 강도가 세지고 계수 값이 줄어들어 조금 과소적합을 유도함.
-그러면 적절한 alpha값은 어떻게 얻을 수 있을까? $R^2$을 그래프로 그려보는 것이다.

```import matploylib.pyplot as plt train_score = [] test_score = [] alpha_list = [0.001,0.01,0.1,1,10,100] for alpha in alpha_list: ridge = Ridge(alpha=alpha) ridge.fit(train_scaled,train_target) train_score.append(ridge.score(train_scaled,train_target)) test_score.appendridge.score(test_scaled,test_target)

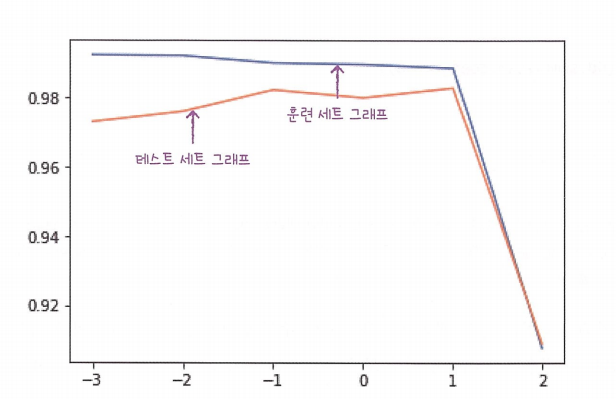
이를 그래프로 그리면 왼쪽이 너무 촘촘하기 때문에, 로그함수로 바꿔 표현

plt.plot(np.log10(alpha_list),train_score) plt.plot(np.log10(alpha_list),test_score) plt.show()

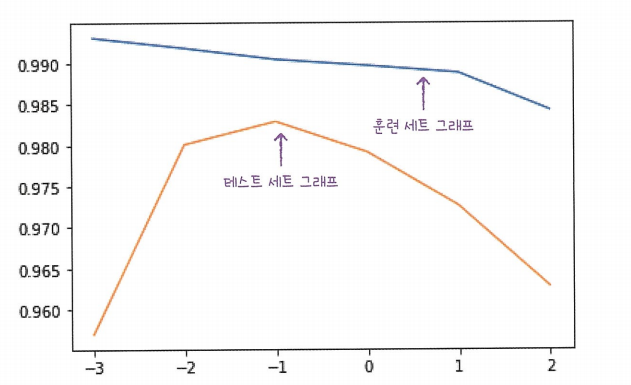
![alt text](../assets/png/plot_3주차.png)
결과를 해석하지면, 테스트 셋 그래프가 -1이후에 성능이 않좋아진다. 따라서 적절한 alpha값은 -1 , 즉 0.1이다. 

ridge=Ridge(alpha=0.1) ridge.fit(train_scaled,train_target) print(ridge.score(train_scaled,train_target)) print(ridge.score(test_scaled,test_target))

0.9903815817570366 0.9827976465386926 ``` 최종 결과는 훈련 세트와 테스트 셋의 점수가 비슷하게 모두 높고 과적합,과소적합 균형을 맞추고 있다.

라쏘 회귀

from sklearn.linear_modle import Lasso
lasso = Lasso()
lasso.fit(train_scaled,train_target)
print(lasso.score(train_scaled,train_target))

> 0.9897898972080961

print(lasso.score(test_scaled,test_target))

> 0.9800593698421883

-alpha값 바꿔서 릿지와 똑같이 수행

train_score = []
test_score = []
alpha_list = [0.001,0.01,0.1,1,10,100]
for alpha in alpha_list:
lasso = Lasso(alpha=alpha,max_iter=10000)
lasso.fit(train_scaled,train_target)
train_score.append(lasso.score(train_scaled,train_target))
test_score.append(lasso.score(test_scaled,test_target))

plt 그리기

plt.plot(np.log10(alpha_list),train_score)
plt.plot(np.log10(alpha_list),test_score)
plt.show()

라쏘 모델에서 최적의 alpha 값은 1 즉 10이다. 이 값으로 다시 훈련

lasso = Lasso(alpha=10)
lasso.fit(train_scaled,train_target)
print(lasso.score(train_scaled,train_target))
print(lasso.score(test_scaled,test_target))

> 0.9888067471131867
> 0.9824470598706695

-coef_속성이 0인 것

print(np.sum(lasso.coef_ ==0))

> 40

Regression Analysis

This post is licensed under CC BY 4.0 by the author.

Chapter3. 회귀 알고리즘과 모델 규제

k-최근접 이웃 회귀

1.데이터셋 불러오기

2.산점도 그리기

3.trainset과 validationset 나누기

결정계수($R^2$)

과대적합 vs 과소적합

선형회귀

데이터 불러오기 및 전처리

선형회귀

다항회귀

특성 공학과 규제

다중회귀

1.Pandas를 활용한 데이터 준비

2.훈련 데이터셋과 테스트 셋으로 나누기

사이킷런의 변환기

다중 회귀 모델 훈련하기

규제

릿지 회귀

라쏘 회귀

Trending Tags